放射線による発がん　解説8

解説8

線量反応

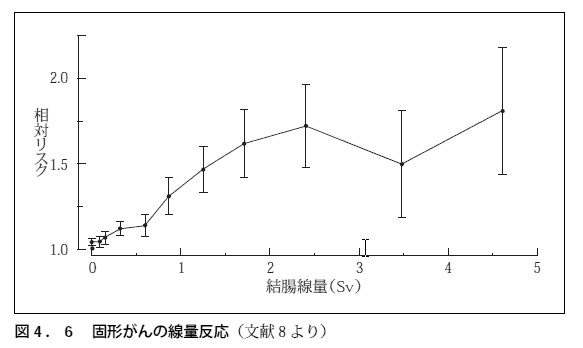
図4.5と図4.6は被曝量とリスクの関係を表したものであり、図4.5が被曝量と白血病の死亡率をグラフ化していて、図 4.6が被曝量と固形ガンの相対リスクをグラフ化しています。折れ線グラフのプロット(●)の上下に描いてあるヒゲの説明がありませんが、こういうグラフでは標準誤差を描くことが多いと思います。標準誤差は信頼区間を計算するためのベースになる値で、90％信頼区間はこの値を約1.6倍したものになり、95％信頼区間はこの値を約2倍したものになります。そしてこの値を1倍したもの、つまりこの値そのものは約70％信頼区間に相当します。

なお何度も説明しているように、図4.6の縦軸は相対リスクではなく死亡率そのものの方が合理的です。

3Sv以上の被曝量では、図4.5は死亡率が低下していて、図4.6はほぼ横ばいになっています。被曝量と死亡率の関係は被曝量と個人的な閾値の割合を累積したものになるという関係から考えると、横ばいは有り得ますが低下は有り得ません。この原因は明らかではないと資料には記載されていますが、被曝量が多い被爆者の数が少ないことが影響しているのではないかと思います。これらの図の標準誤差は被曝量が多くなるほど大きくなっていて、それは対象者数が少ないことを表しています。そして対象者数が少ないと誤差が大きくなるだけでなく、対象者の背景因子が偏る可能性が高くなります。

被曝量と死亡率の関係に低下が有り得ないのは、あくまでも対象者の背景因子が同じという条件の下でのことです。例えば被曝量が多い対象者に若い人が多かったり、女性が多かったり、喫煙者が少なかったりするとガンによる死亡率は低下します。被爆群と非被爆群は、性の割合と年齢が全体としてほぼ一致するように選択されています。しかしそれは全体としてほぼ一致しているだけであり、被爆群を被曝量別にグループ分けした場合、それらのグループの背景因子が全て非被爆群と一致するとは限りません。特に高被曝量グループは人数が少ないため、背景因子に偏りが生じて、他のグループと異なった背景因子を持つ可能性が高くなります。

そしてもし高被曝量グループに死亡率の低い背景因子を持つ人が偏っているとしたら、低被曝量グループには死亡率の高い背景因子を持つ人が偏っていることになります。その結果、高被曝量グループの死亡率は本当の死亡率よりも低くなり、その反対に低被曝量グループの死亡率は本当の死亡率よりも高くなり、被曝量と死亡率の関係が本来の関係をうまく反映しないことになります。ただし低被曝量グループは人数が多いため、背景因子の偏りは高被曝量グループよりも相対的に小さくなり、死亡率の偏りも小さくなると思われます。

そういった背景因子の偏りを補正して被曝量と死亡率の関係を求めるためには、多変量解析という手法を用いる必要があります。しかし多変量解析は、対象者数(特に死亡者数)が少ないと結果の信頼性が低くなるという特徴があります。このデータでも本来は多変量解析を適用し、背景因子の補正をして被曝量と死亡率の関係を検討した方が良いのですが、高被曝量では対象者数が少ないため適用できなかったのかもしれません。

背景因子

このように放射線量だけでなく背景因子の違いも考慮しなければならないところが、医学分野の研究結果を解釈する時の難しさです。そのあたりの事情を知らない人が図4.5を見ると、

「高被曝量では死亡率が低くなるから、2Sv程度の量の放射線を浴びた時は、さらに1Sv程度の放射線を浴びた方が良い」

などと即断してしまうかもしれません。

またガンは生活習慣病であり、性や年齢だけでなく生活環境によって罹患率や死亡率が変化します。そのため特定の地区——例えば原爆が落とされた広島地方や長崎地方、そして原発事故が起きた福島地方——のガンの死亡率は、日本全体のガンの死亡率と一致するとは限りません。そのため放射線の影響を正確に分析するためには、日本全体のガンの死亡率と比較するのではなく、放射線に被曝した人達と同じ地区の、同じ生活習慣の人達のガンの死亡率と比較する必要があります。

この資料では、被爆群と同じ広島地方と長崎地方の被爆していない人の中から、性の割合と年齢がほぼ一致するように非被爆群を選択しています。そのため、この資料のデータは非常に信頼性が高いものになっています。しかし他の放射線の健康被害に関する研究ではそのような配慮をしていない(できない)ものも多く、結果を解釈する時に慎重な検討が必要になります。

このことは医学分野の研究者の間では常識ですが、他の分野(例えば工学分野や物理学分野)の研究者にとっては常識でないため、ややもすると表面的な結果だけ見て、放射線の影響を単純に評価してしまうところがあるように感じられます。